문제
노드가 개인 이진 트리가 있다. 트리를 중위 순회와 유사하게 순회하려고 한다. 이를 유사 중위 순회라고 하자.
순회의 시작은 트리의 루트이고 순회의 끝은 중위 순회할 때 마지막 노드이다. 이때 루트 노드는 항상 1번 노드이다.
유사 중위 순회는 루트 노드에서 시작하며, 다음과 같이 진행된다.
- 현재 위치한 노드의 왼쪽 자식 노드가 존재하고 아직 방문하지 않았다면, 왼쪽 자식 노드로 이동한다.
- 그렇지 않고 현재 위치한 노드의 오른쪽 자식 노드가 존재하고 아직 방문하지 않았다면, 오른쪽 자식 노드로 이동한다.
- 그렇지 않고 현재 노드가 유사 중위 순회의 끝이라면, 유사 중위 순회를 종료한다.
- 그렇지 않고 부모 노드가 존재한다면, 부모 노드로 이동한다.
- 유사 중위 순회를 종료할 때까지 1 ~ 4를 반복한다.
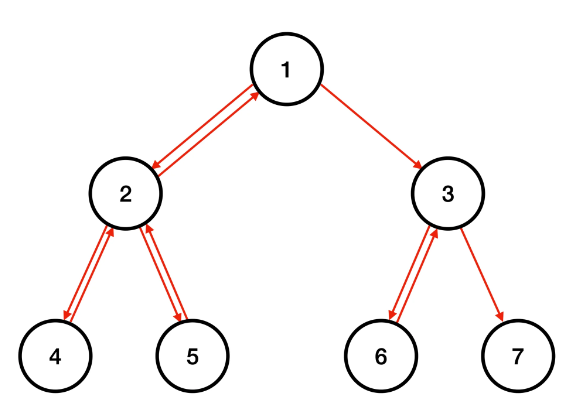
위 그림에 있는 트리에서 중위 순회를 한다면 4→2→5→1→6→3→7 순으로 순회를 한다.
따라서, 유사 중위 순회의 끝은 노드 7이 된다.
유사 중위 순회는 위 그림과 같이 루트인 노드 1에서 시작하여 노드 7에서 끝나고 1→2→4→2→5→2→1→3→6→3→7 이와 같은 순서로 순회를 진행한다. 유사 중위 순회를 진행하면서 총 10번 이동하였다.
여기서 이동이라는 것은 하나의 노드에서 다른 노드로 한번 움직이는 것을 의미한다. 예를 들면, 노드 1에서 노드 2로 가는 것을 한번 이동하였다고 한다.
유사 중위 순회를 하면서 이동한 횟수를 구하려고 한다.
입력
첫 번째 줄에 트리를 구성하는 노드의 개수 이 주어진다.
두 번째 줄부터 번째 줄까지 현재 노드 현재 노드의 왼쪽 자식 노드 , 현재 노드의 오른쪽 자식 노드 가 공백으로 구분되어 주어진다. 만약 자식 노드의 번호가 -1인 경우 자식 노드가 없다는 것을 의미한다.
출력
유사 중위 순회를 하면서 이동한 총 횟수를 출력한다.
해당 문제를 보면 Tree 문제라고 친절하게 알려주고 있다.
추가적으로, 중위순회와 연관된 문제라고 친절하게 알려주고 있다.
※ 중위 순위의 특성 맨마지막 노드는 트리의 오른쪽 맨마지막 노드이다.
이번 문제는 이 특성을 가지고 한 번 해결해보려고 한다.
private static void pseudoInorder(ArrayList<Node> tree, int node) throws IOException {
if (tree.get(node).left != -1) {
CNT++;
pseudoInorder(tree, tree.get(node).left);
CNT++;
}
if (tree.get(node).right != -1) {
CNT++;
pseudoInorder(tree, tree.get(node).right);
CNT++;
}
}
우선 유사 중위 순회를 한다. 왼쪽 노드로 이동하면서 Count++, 왼쪽 노드에서 돌아오면서 Count++ 되는 로직을 그대로 적용한다.
for (int i = 1; tree.get(i).right != -1; i=tree.get(i).right) {
RIGHT_NODE_COUNT++;
}오른쪽 맨마지막 노드로 이동하는 횟수를 구해준다.
BW.write(String.valueOf(CNT - RIGHT_NODE_COUNT));위 두 값을 빼준다.
끝
import java.io.*;
import java.util.*;
class Node {
int left;
int right;
public Node() {
}
}
public class Main {
static BufferedReader BR = new BufferedReader(new InputStreamReader(System.in));
static BufferedWriter BW = new BufferedWriter(new OutputStreamWriter(System.out));
static int N;
static int RIGHT_NODE_COUNT = 0;
static int CNT = 0;
public static void main(String[] args) throws IOException {
StringTokenizer st = new StringTokenizer(BR.readLine());
N = Integer.parseInt(st.nextToken());
ArrayList<Node> tree = new ArrayList<>();
for (int i = 0; i <= N; i++) {
tree.add(new Node());
}
for (int i = 0; i < N; i++) {
st = new StringTokenizer(BR.readLine());
int node = Integer.parseInt(st.nextToken());
tree.get(node).left = Integer.parseInt(st.nextToken());
tree.get(node).right = Integer.parseInt(st.nextToken());
}
for (int i = 1; tree.get(i).right != -1; i=tree.get(i).right) {
RIGHT_NODE_COUNT++;
}
pseudoInorder(tree, 1);
BW.write(String.valueOf(CNT - RIGHT_NODE_COUNT));
BW.flush();
BR.close();
BW.close();
}
private static void pseudoInorder(ArrayList<Node> tree, int node) throws IOException {
if (tree.get(node).left != -1) {
CNT++;
pseudoInorder(tree, tree.get(node).left);
CNT++;
}
if (tree.get(node).right != -1) {
CNT++;
pseudoInorder(tree, tree.get(node).right);
CNT++;
}
}
}
TIP
package com.study.algorithm.boj22856;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.StringTokenizer;
public class Main {
static BufferedReader BR = new BufferedReader(new InputStreamReader(System.in));
static BufferedWriter BW = new BufferedWriter(new OutputStreamWriter(System.out));
static int N;
static int RIGHT_NODE_COUNT = 0;
public static void main(String[] args) throws IOException {
StringTokenizer st = new StringTokenizer(BR.readLine());
N = Integer.parseInt(st.nextToken());
int tree[][] = new int[N+1][2];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(BR.readLine());
int node = Integer.parseInt(st.nextToken());
tree[node][0] = Integer.parseInt(st.nextToken());
tree[node][1] = Integer.parseInt(st.nextToken());
}
for (int i = 1; tree[i][1] != -1; i=tree[i][1]) {
RIGHT_NODE_COUNT++;
}
BW.write(String.valueOf((N - 1) * 2 - RIGHT_NODE_COUNT));
BW.flush();
BR.close();
BW.close();
}
}
Tree의 특성을 이용하면 더 쉽다. Inorder는 모든 Node를 다 방문하므로 Edge의 개수 (N-1) 만큼 반복한다.
Pseudo Inorder를 하면서 2번씩 진행하므로 (N - 1) * 2 번 씩 방문하게 된다.
여기서 Inorder 결과인 오른쪽 노드까지의 엣지수를 빼준다.
결과 : (N - 1) * 2 - RIGHT_NODE_COUNT 로 구할 수 있다.
'알고리즘 > 백준' 카테고리의 다른 글
| [BOJ 1826] 연료 채우기 (0) | 2025.03.31 |
|---|---|
| [BOJ 20207] 달력 (0) | 2025.03.31 |
| 백준 - [BOJ 1865] 웜홀 (0) | 2024.07.06 |
| 백준 - [BOJ 3085] 사탕게임 (0) | 2024.03.01 |
| 백준 - [BOJ 12094] A와 B (0) | 2024.02.29 |


